Evaluating Instruction Set Tradeoffs Quantitatively
While a great deal of research is devoted to CPU performance at the microarchitectural level, I haven’t found much rigorous analysis of performance tradeoffs inherent to the design of instruction sets themselves. And while it’s instructive to examine existing processor instruct sets, without knowing what alternative options were considered, what the tradeoffs where, and ultimately why decisions were made, a lot of important information is missing. For example, one key insight in early research into RISC performance came from analysis of instruction frequencies in common CISC programs. It would found that the more complex instructions were used substantially less frequently than simpler ones.
I’ve decided to explore some of the decisions I made in my own processor design (https://github.com/jbush001/GPGPU) empirically. This processor is targeted by a C++ compiler based on the LLVM toolchain. The beauty of LLVM is that backend code generation is heavily data driven based on templated patterns specified in configuration files processed by a tool called “TableGen.” This makes it relatively easy to quickly make substantial changes to code generation. My experimental methodology is to disable usage of certain instruction set features, and measure the resulting performance of a compiled program.

The test program I used is a 3D renderer implemented in C++. This renders a single frame containing the standard Utah Teapot model with around 2300 triangles into a 512x512 framebuffer using a Phong shading model. It utilizes both hardware multithreading and the wide vector unit. The core engine is around 3000 lines of source code and compiles compiles to 16k of code and 59k of read only data (most of which is geometry data for the model).
All tests are performed measuring the total number of instructions issued while running in the functional simulator. While a cycle accurate simulator of this design is available, this would arguably be heavily microarchitecture dependent and my goal is to evaluate the instruction set . Since instructions have different costs, this is an imperfect measurement. However, it gives a rough idea of the impact of each feature.
I’ve chosen three fundamental features of the instruction set to evaluate.
Feature Analysis
Arithmetic with Immediate Operands
An “immediate” instruction form allows encoding one constant operand directly in the instruction rather than requiring it to first be loaded into a register. For example:
add_i s0, s1, 12
This is fairly common in many architectures, and is useful in a number of common scenarios, such as incrementing or decrementing loop counters or pointers, encoding indices for bit arithmetic, and checking loop counts. In this architecture, the immediate field has a maximum size of 15 bits and a range of 32767 to -32768) Values larger than this must be transferred into a register using a memory load instruction from the read-only section of the program.
One of the big tradeoffs in this architecture is the number of bits each feature takes to be encoded in the instruction and this feature is no exception.
For the first experiment, I disabled arithmetic instructions that utilized this format. These now require an additional instruction to load the value into the register (although the compiler is generally smart enough to retain values across multiple uses, so that cost is amortized over multiple iterations of a loop, for example).
Eliminating immediate arithmetic instructions reduced performance by around 4.2%. This actually turned out to be much smaller than I expected, but is nonetheless arguably large enough to be important.
Baseline 19982553 instructions
No immediate 20869264 instructions
(Lower is better)
One question is whether this instruction format could be replaced by a set of simpler instructions, for example increment and decrement. I instrumented the compiler to dump all of the constants that were emitted during compilation of the test program. There were 124 unique constants used, which would suggest that there is value to having constants encoded.
Mixing Vector and Scalar Operands
One of the features of this instruction set that differs from some more conventional vector architectures is the ability to mix vector and scalar operands. For example:
add_i v0, v2, s1
In this example, the value in scalar register s1 is duplicated across all lanes. There are a number of instances where this is useful, for example, when loop values or parameters are shared among parallel instances of an execution kernel. The tradeoff, as before, is that several additional instruction bits are needed to encode the types of the instruction operands.
Static analysis of the code shows that this feature isn’t used a lot across the entire program, but is used often within core routines that are executed frequently. Disabling this feature requires one extra instruction per use to copy the value from a scalar to vector register first. Running an experiment with this disabled suggested that the feature offers only a 2.1% performance increase.
Baseline 19982553 instructions
No mixing 20405634 instructions
(Lower is better)
Register transfer instructions are relatively cheap (compared to memory operations, for example), so I would expect the impact in a real system to be even smaller.
Register File Size
There is a fair amount of research on how the size of the register file correlates with performance. Although register file size would seem to be a microarchitectural tradeoff (area and energy), it has implications on the instruction set, specifically with the instruction encoding. This design features 32 scalar registers and 32 vector registers. Each register index must be encoded using a 5 bit index. As most operations must encode a destination register, two source registers, and, in the case of vector operations, a mask register, this means 20 bits are consumed by operands alone, leaving only 12 bits to encode the instruction format and operation.
The first experiment I ran varied the number of scalar registers. The difference between the smallest register file in this set (8 registers) and the largest (28 registers) is around 20%, which is significant. The performance curve is relatively smooth: each additional register addition gives an incremental performance improvement:
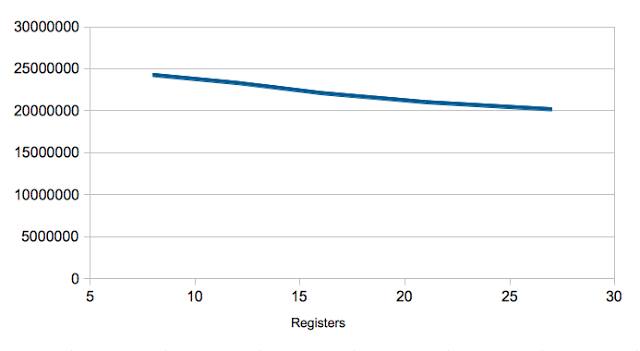
The curve doesn’t appear to be flattening too much near the maximum number of registers, which suggests continuing to add registers would result in additional performance improvements. Unfortunately, to increase available registers above the maximum shown here would require a significant change to the encoding of the instructions.
Performing the same experiment with vector registers gives a much smaller delta. Between 8 and 32 registers, performance only differs by about about 0.3%. Furthermore, above 16 vector registers, the performance is unchanged, as the working values used by this test program apparently fit in that many registers. However, this may be specific to the test program I used; I could contrive classes of programs that would be more heavily dependent on the number of vector registers. I would be interesting to run this test on different types of workloads.
Conclusions
Some of the results were not what I expected. Some fundamental features of the architecture had relatively small overall impacts on performance, although one could argue that the combination of these features may add up to something significant. One thing I didn’t look at much is how these features interact with each other (for example, do the combination of vector/scalar mixing and immediate operands contribute the sum of their individual speed improvements?). Running these tests with different workloads may also yield somewhat different results.